Mathematik3
Stochastik und Statistik
Table of Contents
- 1. Zufall und Wahrscheinlichkeit
- 2. Diskrete Verteilungen
- 3. Stetige Verteilungen
- 4. Parameter
- 5. Deskriptive Statistik
- 6. Schließende Statistik
1. Zufall und Wahrscheinlichkeit
1.1. Wahrscheinlichkeitsraum
Der Wahrscheinlichkeitsraum ist ein Tripel \((\Omega, \mathcal{A}, P)\), wobei \(\Omega\) die Ergebnismenge, \(\mathcal{A}\) die Ereignisalgebra (ereignis systeme) und \(\mathbb{P}\) die Wahrscheinlichkeitsmaß (Verteilung) ist.
1.1.1. Ergebnisraum / Grundraum Ω
Der Ergebnisraum Ω ist die Menge aller möglichen Ergebnisse eines Zufallsexperiments.
Beispiel: Würfel
\Omega = {1, 2, 3, 4, 5, 6}
Ist Ω endlich oder abzählbar, so heißt Ω diskret. (höchstens abzählbar unendlich)
Ist Ω überabzählbar, so heißt Ω stetig. (überabzählbar unendlich)
1.1.2. Ereignisalgebra \(\mathcal{A}\) / σ-Algebra
Die Menge der interesierenden Ereignisse eines Zufallsexperiments (ggf. ist man nicht an allen möglichen teilmengen von \(\Omega\) interessiert).
| Deutsch | Mathematische Darstellung |
|---|---|
| Ereignisse: | \(\mathcal{A} \subseteq 2^\Omega\) |
| Ereignis: | \(A \in 2^\Omega\) |
| Ergebnisse: | \(A \subseteq \Omega\) |
| Ergebnis: | \(\omega \in \Omega\) |
Beispiel: Würfel (wurf einer geraden Zahl)
teilmengen von \Omega: {2, 4, 6}
1.1.3. Wahrscheinlichkeitsmaß \(\mathbb{P}\), Verteilung
Zuweisung einer Wahrscheinlichkeit zu jedem Ereignis in \(\mathcal{A}\).
\[ \forall A \in \mathcal{A}: \mathbb{P}(A) \in [0, 1] \]
sogesehen ist \(\mathbb{P}\) eine Funktion \(\mathcal{A} \to [0, 1]\), die für jedes Ereignis \(A\) die Wahrscheinlichkeit \(\mathbb{P}(A)\) angibt.
\[ \mathbb{P} \colon \mathcal{A} \to [0, 1] \]
- Rechenregeln
- endliche Additivität:
für endlich viele Ereignisse, die alle paarweise disjunkt sind, ist die wahrscheinlichkeit der Vereinigung gleich der Summe der Wahrscheinlichkeiten der einzelnen Ereignisse.
\[ \mathbb{P} \left( \bigcup_{i=1}^n A_i \right) = \sum_{i=1}^n \mathbb{P}(A_i) \]
- gegenwahrscheinlichkeit:
\[ \forall A \in \mathcal{A}: \mathbb{P}(A^c) = 1 - \mathbb{P}(A) \]
- vereinigung zweier Ereignisse:
\[ \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B) \]
- vereinigung mehrerer Ereignisse:
Sieb-formel von Poincaré und Sylvester (inkl. Inklusion-Exklusion):
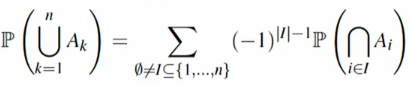
- subadditivität:
die wahrscheinlichkeit der Vereinigung ist immer nach oben beschränkt durch die Summe der Wahrscheinlichkeiten der einzelnen Ereignisse. (überlappung, überdeckung)
\[ \mathbb{P} \left( \bigcup_{i=1}^n A_i \right) \le \sum_{i=1}^n \mathbb{P}(A_i) \]
- monotonie:
für zwei Ereignisse \(A\) und \(B\) mit \(A \subseteq B\) gilt:
\[ \mathbb{P}(A) \le \mathbb{P}(B) \]
denn man kann die Mengen paarweise disjunkt zerlegen und additive Eigenschaften nutzen.
1.2. Wahrscheinlichkeitsbegriff (Bayessher und frequentistischer)
1.2.1. Klassischer Wahrscheinlichkeitsbegriff
Pascal, Fermat, Bernoulli, Laplace
Anzahl der günstigen Fälle durch Anzahl der möglichen Fälle.
Die Wahrscheinlichkeit eines Ereignisses \(A\):
\[ \mathbb{P}(A) = \frac{| A |}{| \Omega |} \]
unter der Annahme, dass alle Ergebnisse gleich wahrscheinlich sind.
1.2.2. Statistischer Wahrscheinlichkeitsbegriff
Pascal, Fermat, Bernoulli, Laplace
Die Wahrscheinlichkeit eines Ereignisses \(A\), welches zufällig auftritt:
\[ \mathbb{P}(A) = \lim_{n \to \infty} \frac{n_A}{n} \]
mit
\[ n_A = | \{ \forall i \in [1, n] \colon A \text{ triff im i-ten Versuch ein} \} | \]
wobei \(n_A\) die Anzahl der günstigen Fälle und \(n\) die Anzahl der möglichen Fälle (Versuche) ist. Dieser Grenzwert beschreibt die relative Häufigkeit des Ereignisses \(A\).
Der Grenzwert der relativen Häufigkeit muss nicht immer existieren und ist auch nicht immer eindeutig.
Die durchführung einer hohe Anzahl von Versuchen ist nicht immer möglich.
1.2.3. Bayesscher Wahrscheinlichkeitsbegriff
Subjective Wahrscheinlichkeit, die auf degree of belief basiert.
Der Überzeugungsgrad kann sich ändern (update of beliefs).
- a priori Wahrscheinlichkeit von \(A\): bevor Daten bekannt sind / beobachtet wurden
- a posteriori Wahrscheinlichkeit von \(A\): nachdem Daten bekannt sind / beobachtet wurden
Je mehr Informationen, desto besser die Schätzung (*degree of belief*).
1.2.4. Axiomatische Wahrscheinlichkeitstheorie
Kolmogoroff
- Nicht-Negativität: \(\mathbb{P}(A) \ge 0\) für alle \(A \in \mathcal{A}\)
- Normiertheit: \(\mathbb{P}(\Omega) = 1\)
- σ-Additivität: \(\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B)\) für alle \(A, B \in \mathcal{A}\) mit \(A \cap B = \emptyset\)
oder auch:
Für jede Folge \((A_n)_{n \in \mathbb{N}}\) mit \(A_n \in \mathcal{A}\) und \(A_i \cap A_j = \emptyset\) für \(i \ne j\) gilt:
\[ \mathbb{P} \left( \bigcup_{n\in \mathbb{N}} A_n \right) = \sum_{n \in \mathbb{N}} \mathbb{P}(A_n) \]
1.3. Bedingte Wahrscheinlichkeiten und Stochastische Unabhengigkeit
TODO: vl2 ab 26min
2. Diskrete Verteilungen
2.1. Laplace-Verteilung
2.2. Poisson-Verteilung
2.3. Bernoulli-Verteilung
3. Stetige Verteilungen
3.1. Normal-, Standardnormalverteilung und Student-t-Verteilung
3.2. Chi-Quadrat-Verteilung
4. Parameter
4.1. Erwartungswert, Varianz, Standardabweichung, Schiefe, Wölbung
4.2. Ungleichungen (Chebyshev, Chernov, Markov)
5. Deskriptive Statistik
- Skaletypen: Nominal, Ordinal, Intervall, Verhältnis
- Modus: Wert, der am häufigsten vorkommt
- Median: Wert, der in der Mitte liegt
- Mittelwert: Durchschnittswert
- empirische Varianz: Streuung der Werte
- empirische Standardabweichung: Wurzel der Varianz
- momente: Erwartungswert, Varianz, Schiefe, Wölbung